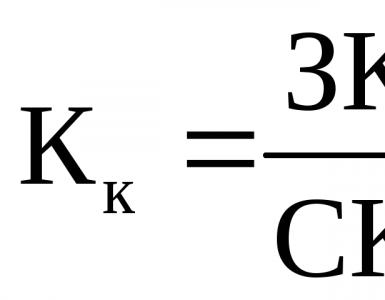Ее величиной и. Понятие величины и её измерения в математике. По форме различают статистические показатели

Натуральное число как мера величины

Известно, что числа возникли из потребности счета и измерения, но если для счета достаточно натуральных чисел, то для измерения величин нужны и другие числа. Однако в качестве результата измерения величин будем рассматривать только натуральные числа. Определив смысл натурального числа как меры величины, мы выясним, какой смысл имеют арифметические действия над такими числами. Эти знания нужны учителю начальных классов не только для обоснования выбора действий при решении задач с величинами, но и для понимания еще одного подхода к трактовке натурального числа, существующего в начальном обучении математике.

Натуральное число мы будем рассматривать в связи с измерением положительных скалярных величин - длин, площадей, масс, времени и др, поэтому прежде, чем говорить о взаимосвязи величин и натуральных чисел, напомним некоторые факты, связанные с величиной и ее измерением, тем более что понятие величины, наряду с числом, является основным в начальном курсе математики.

Понятие положительной скалярной величины и ее измерения

Рассмотрим два высказывания, в которых используется слово «длина»:

1) Многие окружающие нас предметы имеют длину.

2) Стол имеет длину.

В первом предложении утверждается, что длиной обладают объекты некоторого класса. Во втором речь идет о том, что длиной обладает конкретный объект из этого класса. Обобщая, можно сказать, что термин «длина» употребляется для обозначения свойства , либо класса объектов (предметы имеют длину), либо конкретного объекта из этого класса (стол имеет длину).

Но чем это свойство отличается от других свойств объектов этого класса? Так, например, стол может иметь не только длину, но и быть изготовленным из дерева или металла; столы могут иметь разную форму. О длине можно сказать, что разные столы обладают этим свойством в разной степени (один стол может быть длиннее или короче другого), чего не скажешь о форме - один стол не может быть «прямоугольнее» другого.

Таким образом, свойство «иметь длину» - особое свойство объектов, оно проявляется тогда, когда объекты сравнивают по их протяженности (по длине). В процессе сравнения устанавливают, что либо два объекта имеют одну и ту же длину, либо длина одного меньше длины другого.

Аналогично можно рассматривать и другие известные величины: площадь, массу, время и т.д. Они представляют собой особые свойства окружающих нас предметов и явлений и проявляются при сравнении предметов и явлений по этому свойству, причем каждая величина связана с определенным способом сравнения.

Величины, которые выражают одно и тоже свойство объектов, называются величинами одного рода или однородными величинами . Например, длина стола и длина комнаты - это величины одного рода.

Напомним основные положения, связанные с однородными величинами.

1. Любые две величины одного рода сравнимы: они либо равны, либо одна меньше другой. Другими словами, для величин одного рода имеют место отношения «равно», «меньше» и «больше», и для любых величин А и В справедливо одно и только одно из отношений: А<В, А = В, А> В.

Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем длина любого катета этого треугольника, масса яблока меньше массы арбуза, а длины противоположных сторон прямоугольника равны.

2. Отношение «меньше» для однородных величин транзитивно: если А < В и В < С, то А < С.

Так, если площадь треугольника F 1 меньше площади треугольника F 2 , и площадь треугольника F 2 меньше площади треугольника F 3 , то площадь треугольника F 1 меньше площади треугольника F 3 .

3. Величины одного рода можно складывать, в результате сложения получается величина того же рода. Иными словами, для любых двух величин А и В однозначно определяется величина С = А + В, которую называют суммой величин А и В.

Сложение величин коммутативно и ассоциативно.

Например, если А - масса арбуза, а В - масса дыни, то С = А +В - это масса арбуза и дыни. Очевидно, что А+В = В+А и(А+В) + С = А+(В+С).

Разностью величин А и В называется такая величина

С = А - В, что А = В + С.

Разность величин А и В существует тогда и только тогда, когда А>В.

Например, если А - длина отрезка а, В - длина отреза b, то С=А-В - это длина отрезка с (рис. 1).

5. Величину можно умножать на положительное действительное число, в результате получают величину того же рода. Более точно, для любой величины А и любого положительного действительного числа х существует единственная величина В =

х. А, которую называют произведением величины А на число х.

Например, если А - время, отводимое на один урок, то умножив А на число х = 3, получим величину В = 3·А - время, за которое пройдет 3 урока.

6. Величины одного рода можно делить, получая в результате число. Определяют деление через умножение величины на число.

Частным величин А и В называется такое положительное действительное число х = А: В, что А =х·В.

Так, если А - длина отрезка а, В - длина отрезка b (рис. 2) и отрезок А состоит из 4-х отрезков, равных b, то А:В = 4, поскольку А= 4·В.

Величины, как свойства объектов, обладают еще одной особенностью - их можно оценивать количественно. Для этого величину надо измерить. Чтобы осуществить измерение из данного рода величин выбирают величину, которую называют единицей измерения. Мы будем обозначать ее буквой Е.

Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А - это значит найти такое положительное действительное число х, что А =х·Е .

Число х называется численным значением величины А при единице величины Е. Оно показывает, во сколько раз величина А больше (или меньше) величины Е, принятой за единицу измерения.

Если А=х·Е, то число х называют также мерой величины А при единице Е и пишут х=m Е (А).

Например, если А - длина отрезка а, Е- длина отрезка b (рис.2), то А=а·Е. Число 4 - это численное значение длины А при единице длины Е, или, другими словами, число 4 - это мера длины А при единице длины Е.

В практической деятельности при измерении величин люди пользуются стандартными единицами величин: так, длину измеряют в метрах, сантиметрах и т.д. Результат измерения записывают в таком виде: 2,7 кг; 13 см; 16 с. Исходя из понятия измерения, данного выше, эти записи можно рассматривать как произведение числа и единицы величины. Например, 2,7 кг = 2,7·кг; 13 см = 13·см; 16 с = 16·с.

Используя это представление, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, например, требуется выразить ч в минутах. Так как ч = · ч и час = 60 мин, то ч = ·60·мин = ( · 60) мин = 25 мин.

Величина, которая определяется одним численным значением, называется скалярной величиной .

Если при выбранной единице измерения скалярная величина принимает только положительные численные значения, то ее называют положительной скалярной величиной.

Положительными скалярными величинами являются длина, площадь, объем, масса, время, стоимость и количество товара и др.

Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от действий над величинами к соответствующим действиям над числами, и наоборот.

1. Если величины А и В измерены при помощи единицы величины Е, то отношения между величинами А и В будет такими же, как и отношения между их численными значениями, и наоборот:

А+В <=> m(А)+ m(В);

А<В <=> m (А)

А> В <=> m (А) > m (В).

Например, если массы двух тел таковы, что А =5 кг, В=3 кг, то можно утверждать, что А> В, поскольку 5 > 3.

2. Если величины А и В измерены при помощи единицы величины Е, то чтобы найти численное значение суммы А + В, достаточно сложить численные значения величин А и В:

А + В = С <=> m (А +В) = m (А) + m (В). Например, если А = 5 кг, В = 3 кг, то А + В = 5 кг + 3 кг = = (5 + 3) кг = 8 кг.

3. Если величины А и В таковы, что В= х·А, где х - положительное действительное число, и величина А измерена при помощи единицы величины Е, то, чтобы найти численное значение величины В при единицы Е, достаточно число х умножить на число m (А):

В = х·А <=> m (В)=х·m(А).

Например, если масса В в 3 раза больше массы А и А = 2 кг, то В = 3А = 3· (2·кг) = (3·2)кг = 6 кг.

В математике при записи произведения величины А на число х принято число писать перед величиной, т.е. х·А. Но разрешается писать и так: Ах. Тогда численное значение величины А умножают на х, если находят значение величины А·х.

Рассмотренные понятия - объект (предмет, явление, процесс), его величина, численное значение величины, единица величины - надо уметь вычленять в текстах и задачах. Например, математическое содержание предложения «Купили 3 килограмма яблок» можно описать следующим образом: в предложении рассматривается такой объект, как яблоки, и его свойство - масса; для измерения массы использовали единицу массы -килограмм; в результате измерения получили число 3 - численное значение массы яблок при единице массы - килограмм.

Один и тот же объект может обладать несколькими свойствами, которые являются величинами. Например, для человека - это рост, масса, возраст и др. Процесс равномерного движения характеризуется тремя величинами: расстоянием, скоростью и временем, между которыми существуют зависимость, выражаемая формулой s = v·t.

Если величины выражают разные свойства объекта, то их называют величинами разного рода , или разнородными величинами . Так, например, длина и масса - это разнородные величины.

Это первоначальное понятие величины является непосредственным обобщением более конкретных понятий: длины, площади, объёма, массы и т. п. Каждый конкретный род величины связан с определённым способом сравнения физических тел или др. объектов. Например, в геометрии отрезки сравниваются при помощи наложения, и это сравнение приводит к понятию длины: два отрезка имеют одну и ту же длину , если при наложении они совпадают; если же один отрезок накладывается на часть другого, не покрывая его целиком, то длина первого меньше длины второго. Общеизвестны более сложные приёмы, необходимые для сравнения плоских фигур по площади или пространственных тел по объёму .

Свойства

В соответствии со сказанным, в пределах системы всех однородных величин (то есть в пределах системы всех длин или всех площадей, всех объёмов) устанавливается отношение порядка : две величины а и b одного и того же рода или совпадают (а = b) , или первая меньше второй (а < b ), или вторая меньше первой (b < a ). Общеизвестно также в случае длин, площадей, объёмов и то, каким образом устанавливается для каждого рода величины смысл операции сложения. В пределах каждой из рассматриваемых систем однородных величин отношение а < b и операция а + b = с обладают следующими свойствами:

1. Каковы бы ни были а и b , имеет место одно и только одно из трёх соотношений: или а = b , или а < b , или b < a
2. Если а < b и b < c , то а < с (транзитивность отношений «меньше», «больше»)
3. Для любых двух величин а и b существует однозначно определённая величина с = а+b
4. а + b = b+ а (коммутативность сложения)
5. а + (b + с) = (а + b)+ с (ассоциативность сложения)
6. а + b > а (монотонность сложения)
7. Если а > b , то существует одна и только одна величина с , для которой b + с = а (возможность вычитания)
8. Каковы бы ни были величины а и натуральное число n , существует такая величина b , что nb = a (возможность деления)
9. Каковы бы ни были величины а и b , существует такое натуральное число n , что а < nb . Это свойство называется аксиомой Евдокса , или аксиомой Архимеда . На нём вместе с более элементарными свойствами 1-8 основана теория измерения величин, развитая древнегреческими математиками.

Если взять какую-либо длину l за единичную, то система s" всех длин, находящихся в рациональном отношении к l , удовлетворяет требованиям 1-9. Существование несоизмеримых (см. Соизмеримые и несоизмеримые величины) отрезков (открытие которых приписывается Пифагору, 6 в. до н. э.) показывает, что система s" ещё не охватывает системы s всех вообще длин.

Чтобы получить вполне законченную теорию величин, к требованиям 1-9 надо присоединить ещё ту или иную дополнительную аксиому непрерывности, например:

10) Если последовательности величин a1 обладают тем свойством, что bn - an < с для любой величины с при достаточно большом номере n , то существует единственная величина х , которая больше всех an и меньше всех bn .

Свойства 1-10 и определяют полностью современное понятие системы положительных скалярных величин. Если в такой системе выбрать какую-либо величину l за единицу измерения, то все остальные величины системы однозначно представляются в виде а = al , где а - положительное действительное число.

Другие подходы

См. также

Wikimedia Foundation . 2010 .

Синонимы :

Смотреть что такое "Величина" в других словарях:

Сущ., ж., употр. сравн. часто Морфология: (нет) чего? величины, чему? величине, (вижу) что? величину, чем? величиной, о чём? о величине; мн. что? величины, (нет) чего? величин, чему? величинам, (вижу) что? величины, чем? величинами, о чём? о… … Толковый словарь Дмитриева

ВЕЛИЧИНА, величины, мн. величины, величинам (книжн.), и (разг.) величины, величинам, жен. 1. только ед. Размер, объем, протяжение вещи. Величина стола достаточная. Комната громадной величины. 2. Всё, что можно измерить и исчислить (мат. физ.).… … Толковый словарь Ушакова

Размер, формат, калибр, доза, рост, объем, протяжение. Ср … Словарь синонимов

Ы; мн. чины; ж. 1. только ед. Размер (объём, площадь, протяжённость и т.п.) какого л. объекта, предмета, имеющего видимые физические границы. В. здания. В. стадиона. Величиной с булавку. Величиной в ладонь. Отверстие большей величины. В… … Энциклопедический словарь

величина - ВЕЛИЧИНА1, ы, ж Разг. О человеке, выделяющемся среди других, выдающемся в какой л. области деятельности. Н. Коляда крупная величина в современной драматургии. ВЕЛИЧИНА2, ы, мн величины, ж Размер (объем, протяженность, площадь) предмета, который… … Толковый словарь русских существительных

Современная энциклопедия

ВЕЛИЧИНА, ы, мн. ины, ин, жен. 1. Размер, объём, протяжённость предмета. Площадь большой величины. Измерить величину чего н. 2. То, что можно измерить, исчислить. Равные величины. 3. О человеке, выдающемся в какой н. области деятельности. Этот… … Толковый словарь Ожегова

величина - ВЕЛИЧИНА, размер, размеры … Словарь-тезаурус синонимов русской речи

Величина - ВЕЛИЧИНА, обобщение конкретных понятий: длины, площади, веса и т.д. Выбор одной из величин данного рода (единицы измерения) позволяет сравнивать (соизмерять) величины. Развитие понятия величина привело к скалярным величинам, характеризующимся… … Иллюстрированный энциклопедический словарь

В математике 1) обобщение конкретных понятий: длины, площади, веса и т. п. Выбрав одну из величин данного рода за единицу измерения, можно выразить числом отношение любой другой величины того же рода к единице измерения.2) В более общем смысле… … Большой Энциклопедический словарь

Величина, ы; мн. величины, ин … Русское словесное ударение

Книги

• Величина , Вилюнова В. (ред.) , Эта замечательная книжка, созданная для самых маленьких читателей, предназначена для развития речи и мышления. Крупные, яркие картинки на разноцветных страничкахзнакомят ребенка с понятиями… Категория:

Длина, площадь, масса, время, объём – величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием.

Величина – это особое свойство реальных объектов или явлений, и особенность заключается в том, что это свойство можно измерить, то есть назвать количество величины. Величины, которые выражают одно и тоже свойство объектов, называются ве­личинами одного рода или однородными величинами . Например, длина стола и дли на комнаты – это однородные величины. Величины – длина, площадь, масса и другие обладают рядом свойств.

1) Любые две величины одного рода сравнимы: они либо равны, либо одна меньше (больше) другой. То есть, для величин одного рода имеют место отношения «равно», «меньше», «больше» и для любых величин и справедливо одно и только одно из отношений: Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем любой катет данного треугольника; масса лимона меньше, чем масса арбуза; длины противоположных сторон прямоугольника равны.

2) Величины одного рода можно складывать, в результате сложения получится величина того же рода. Т.е. для любых двух величин а и b однозначно определяется величина a+b, её называют суммой величин а и b. Например, если a-длина отрезка AB, b – длина отрезка ВС (рис.1), то длина отрезка АС, есть сумма длин отрезков АВ и ВС;

3) Величину умножают на действительное число, получая в результате величину того же рода. Тогда для любой величины а и любого неотрицательного числа x существует единственная величина b= x а, величину b называют произведением величины а на число x. Например, если a – длину отрезка АВ умножить на

x= 2, то получим длину нового отрезка АС.(Рис.2)

4) Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а=b+c. Например, если а – длина отрезка АС, b – длина отрезка AB, то длина отрезка ВС есть разность длин отрезков и АС и АВ.

5) Величины одного рода делят, определяя частное через произведение величины на число; частным величин а и b-называется такое неотрицательное действительное число х, что а= х b. Чаще это число – называют отношением величин а и b и записывают в таком виде: a/b = х. Например, отношение длины отрезка АС к длине отрезка АВ равно 2.(Рис №2).

6) Отношение «меньше» для однородных величин транзитивно: если А<В и В<С, то А<С. Так, если площадь треугольника F1 меньше площади треугольника F2 площадь треугольника F2 меньше площади треугольника F3, то площадь треугольника F1 меньше площади треугольника F3.Величины, как свойства объектов, обладают ещё одной особенностью – их можно оценивать количественно. Для этого величину нужно измерить. Измерение – заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. В результате измерения получают число, которое называют численным значением при выбранной единице.

Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей – другой, для масс- третий и так далее. Но каким бы ни был этот процесс, в результате измерения величина получает определённое численное значение при выбранной единице.

Вообще, если дана величина а и выбрана единица величины e, то в результате измерения величины а находят такое действительное число x, что а=x e. Это число x называют численным значением величины а при единице е. Это можно записать так: х=m (a).

Согласно определению любую величину можно представить в виде произведения некоторого числа и единицы этой величины. Например, 7 кг = 7∙1 кг, 12 см =12∙1 см, 15ч =15∙1 ч. Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, например, требуется выразить 5/12ч в минутах. Так как, 5/12ч = 5/12 60мин = (5/12 ∙ 60)мин = 25мин.

Величины, которые вполне определяются одним численным значением, называются скалярными величинами. Такими, к примеру, являются длина, площадь, объём, масса и другие. Кроме скалярных величин, в математике рассматривают ещё векторные величины. Для определения векторной величины необходимо указать не только её численное значение, но и направление. Векторными величинами являются сила, ускорение, напряжённость электрического поля и другие.

В начальной школе рассматриваются только скалярные величины, причём такие, численные значения которых положительны, то есть положительные скалярные величины.

Измерение величин позволяет свести сравнение их к сравнению чисел, операции над величинами к соответствующим операциям над числами.

1/.Если величины а и b измерены при помощи единицы величины e, то отношения между величинами a и b будут такими же, как и отношения между их численными значениями, и наоборот.

A=b m (a)=m (b),

A>b m (a)>m (b),

A

Например, если массы двух тел таковы, что а=5 кг, b=3 кг, то можно утверждать, что масса а больше массы b поскольку 5>3.

2/ Если величины а и b измерены при помощи единицы величины e, то, чтобы найти численное значение суммы a+b достаточно сложить

численные значения величин а и b. а+b= c m (a+b) = m (a) + m (b). Например, если а = 15 кг, b=12 кг, то а+b=15 кг + 12 кг = (15+12) кг = 27кг

З/ Если величины а и b таковы, что b= x а, где x -положительное действительное число, и величина а, измерена при помощи единицы величины e, то чтобы найти численное значение величины b при единице e, достаточно число x умножить на число m (а):b=x a m (b)=x m (a).

Например, если масса а в 3 раза больше массы b, т.е. b = За и а = 2 кг, то b = За = 3 ∙ (2 кг) = (3∙2) кг = 6 кг.

Рассмотренные понятия – объект, предмет, явление, процесс, его величина, численное значение величины, единица величины – надо уметь вычленять в текстах и задачах.

Например, математическое содержание предложения «Купили 3 килограмма яблок» можно описать следующим образом: в предложении рассматривается такой объект, как яблоки, и его свойство – масса; для измерения массы использовали единицу массы – килограмм; в результате измерения получили число 3 -численное значение массы яблок при единице массы – килограмм.

Рассмотрим определения некоторых величин и их измерений.

Из курса математики нам известны действия, которые можно производить над числами. Складывать, вычитать и сравнивать в математике можно любые числа. Такие действия над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.

Например:

4 м + 3 м = 7 м;
9 кг - 5 кг = 4 кг;
30 с > 10 с.

Во всех трех случаях мы производили действия над однородными физическими величинами. Складывали длину с длиной, вычитали из массы массу, сравнивали промежуток времени с промежутком времени. Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг!

А вот умножать и делить можно не только однородные, но и разные физические величины. Например:

1. 10 кг ÷2 кг = 5. Здесь делятся не только числовые значения (10 ÷ 2 = 5), но и единицы физических величин (кг ÷ кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.
2. 2 м. 4 м = 8 м 2 . Умножаются числовые значения (2 . 4 = 8) и единицы физических величин (м. м = м 2). В результате умножения двух физических величин - длин l 1 = 2 м и l 2 = 4 м - получилась новая физическая величина - площадь S = 8 м 2 .
3. 10 м ÷ 2 с = 5 м/с. В результате деления двух разных физических величин - длины l = 10 м на промежуток времени t = 2 с, получилась новая физическая величина 5 м/c. Ее числовое значение равно 5, а единица новой физической величины - м/c. Эта физическая величина v = 5 м/c - скорость.
4. 10 м ÷ 2 с = 20 м ÷ 4 с. Знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 10 м ÷ 2 с и 20 м ÷ 4 мин. Здесь м/с ≠ м/мин.

Подумайте и ответьте

1. Что необходимо учитывать при сложении и вычитании физических величин? Каким будет результат их сложения и вычитания?
2. Какие физические величины можно сравнивать между собой? Приведите примеры.
3. Можно ли делить и умножать разные физические величины? Что получится в результате?
4. Определите, значение какой физической величины получится в результате:
   1. 40 с - 10 с;
   2. 40 c ÷ 10 c;
   3. 3 м. 4 м. 2 м;
   4. 120 км ÷ 2 ч.

Интересно знать!

Большие единицы времени - год и сутки - дала нам сама природа. Но час, минута и секунда появились благодаря человеку.

Принятое в настоящее время деление суток восходит к глубокой древности. В Вавилоне применялась не десятичная, а шестидесятеричная система счисления. Шестьдесят делится без остатка на 12, отсюда у вавилонян деление суток на 12 равных частей. В Древнем Египте было введено деление суток на 24 часа. Позже появились минуты и секунды. То, что в 1 часе 60 минут, а в 1 минуте 60 секунд, - также наследие шестидесятеричной системы Вавилона.

Определение единиц времени является очень важным. Основная единица времени - секунда - сначала была введена как 1/86400 доля суток, а затем из-за непостоянства суток - как определенная доля года. В настоящее время эталон секунды связан с частотой излучения атомов цезия.

Физической величиной называется физическое свойство материального объекта, процесса, физического явления, охарактеризованное количественно.

Значение физической величины выражается одним или несколькими числами, характеризующими эту физическую величину, с указанием единицы измерения.

Размером физической величины являются значения чисел, фигурирующих в значении физической величины.

Единицы измерения физических величин.

Единицей измерения физической величины является величина фиксированного размера, которой присвоено числовое значение, равное единице. Применяется для количественного выражения однородных с ней физических величин. Системой единиц физических величин называют совокупность основных и производных единиц, основанную на некоторой системе величин.

Широкое распространение получило всего лишь некоторое количество систем единиц. В большинстве случаев во многих странах пользуются метрической системой.

Основные единицы.

Измерить физическую величину - значит сравнить ее с другой такой же физической величиной, принятой за единицу.

Длину предмета сравнивают с единицей длины, массу тела - с единицей веса и т.д. Но если один исследователь измерит длину в саженях, а другой в футах, им будет трудно сравнить эти две величины. Поэтому все физические величины во всем мире принято измерять в одних и тех же единицах. В 1963 году была принята Международная система единиц СИ (System international - SI).

Для каждой физической величины в системе единиц должна быть предусмотрена соответствующая единица измерения. Эталоном единицы измерения является ее физическая реализация.

Эталоном длины является метр - расстояние между двумя штрихами, нанесенными на стержне особой формы, изготовленном из сплава платины и иридия.

Эталоном времени служит продолжительность какого-либо правильно повторяющегося процесса, в качестве которого выбрано движение Земли вокруг Солнца: один оборот Земля совершает за год. Но за единицу времени принимают не год, а секунду .

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за 1 с совершает перемещение в 1 м.

Отдельная единица измерения используется для площади, объема, длины и т. д. Каждая единица определяется при выборе того или иного эталона. Но система единиц значительно удобнее, если в ней в качестве основных выбрано всего несколько единиц, а остальные определяются через основные. Например, если единицей длины является метр, то единицей площади будет квадратный метр, объема - кубический метр, скорости - метр в секунду и т. д.

Основными единицами физических величин в Международной системе единиц (СИ) являются: метр (м), килограмм (кг), секунда (с), ампер (А), кельвин (К), кандела (кд) и моль (моль).

Основные единицы СИ
Величина	Единица	Обозначение
	Наименование	русское	международное
Сила электрического тока
Термодинамическая температура
Сила света
Количество вещества

Существуют также производные единицы СИ, у которых есть собственные наименования:

Производные единицы СИ, имеющие собственные наименования
	Единица		Выражение производной единицы
Величина	Наименование	Обозначение	Через другие единицы СИ	Через основные и дополнительные единицы СИ
Давление				м -1 ЧкгЧс -2
Энергия, работа, количество теплоты				м 2 ЧкгЧс -2
Мощность, поток энергии				м 2 ЧкгЧс -3
Количество электричества, электрическийзаряд
Электрическое напряжение, электрическийпотенциал				м 2 ЧкгЧс -3 ЧА -1
Электрическая емкость				м -2 Чкг -1 Чс 4 ЧА 2
Электрическое сопротивление				м 2 ЧкгЧс -3 ЧА -2
Электрическая проводимость				м -2 Чкг -1 Чс 3 ЧА 2
Поток магнитной индукции				м 2 ЧкгЧс -2 ЧА -1
Магнитная индукция				кгЧс -2 ЧА -1
Индуктивность				м 2 ЧкгЧс -2 ЧА -2
Световой поток
Освещенность				м 2 ЧкдЧср
Активность радиоактивного источника	беккерель
Поглощенная доза излучения

И змерения . Для получения точного, объективного и легко воспроизводимого описания физической величины используют измерения. Без измерений физическую величину нельзя охарактеризовать количественно. Такие определения, как «низкое» или «высокое» давление, «низкая» или «высокая» температура отражают лищь субъективные мнения и не содержат сравнения с эталонными величинами. При измерении физической величины ей приписывают некоторое численное значение.

Измерения осуществляются с помощью измерительных приборов. Существует довольно большое количество измерительных приборов и приспособлений, от самых простых до сложных. Например, длину измеряют линейкой или рулеткой, температуру - термометром, ширину - кронциркулем.

Измерительные приборы классифицируются: по способу представления информации (показывающие или регистрирующие), по методу измерений (прямого действия и сравнения), по форме представлений показаний (аналоговый и цифровой), и др.

Для измерительных приборов характерны следующие параметры:

Диапазон измерений - область значений измеряемой величины, на которой рассчитан прибор при его нормальном функционировании (с заданной точностью измерения).

Порог чувствительности - минимальное (пороговое) значение измеряемой величины, различаемое прибором.

Чувствительность - связывает значение измеряемого параметра и соответствующее ему изменение показаний прибора.

Точность - способность прибора указывать истинное значение измеряемого показателя.

Стабильность - способность прибора поддерживать заданную точность измерений в течение определенного времени после калибровки.