Решение кратных интегралов. Кратные интегралы. Смена порядка интегрирования

Транскрипт

1 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика СП КОРОЛЕВА» КРАТНЫЕ ИНТЕГРАЛЫ задачи и упражнения Утверждено Редакционно-издательским советом университета в качестве методических указаний С А М А Р А Издательство СГАУ

2 УДК 7 7 Составитель ОМ Карпилова Рецензент канд техн наук доц Г Н Г у т м а н Кратные интегралы задачи и упражнения: метод указания / сост ОМ Карпилова Самара: Изд-во Самар гос аэрокосм ун-та с Сборник содержит образцы решения типовых задач по темам: двойные интегралы тройные интегралы приложения кратных интегралов В каждой теме рассматриваются типовые задачи подробно разбираются методы их решения и предлагаются задачи для самостоятельной работы В приложении даны варианты индивидуального домашнего задания Все задания составлены в соответствии с программой по курсу математики для студентов технических вузов Методические указания подготовлены на кафедре общей инженерной подготовки и предназначены для студентов института энергетики и транспорта Самарского государственного аэрокосмического университета УДК 7 7 Самарский государственный аэрокосмический университет

3 ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ Для вычисления двойного интеграла его представляют в виде повторного двукратного интеграла f f Решение примеров Пример Перейти от b a f к повторному интегралу и расставить пределы интегрирования если область ограничена линиями: а 6; б; в; г контуром треугольника ABC где A; B;6 C;; д Решение: а Построим область: прямая параллельная оси О; прямая параллельная оси О; 6 прямая проходящая через точки;6 и 6; Область это треугольник АВС рис Чтобы найти координаты точки С надо решить систему уравнений Рис 6 Отсюда С; Поэтому внутри области Чтобы выяснить как изменяется проведем прямую параллельную оси O и пересекающую область Эта прямая входит в область по линии а выходит по линии 6 или 6 Поэтому 6 Таким образом область можно задать системой неравенств: 6 Теперь легко расставить пределы в двукратном интеграле: f 6 f

4 б Построим: парабола прямая параллельная оси O рис Найдем координаты точек А и В Для этого решим систему ± Проведем прямую параллельную оси O и пересекающую область Эта линия входит в область по параболе и выходит по прямой Рис Таким образом область задается неравенствами f f: Поэтому в Построим область рис: парабола симметричная относительно оси O с вершиной в начале координат; положительная ветвь параболы у симметричной относительно оси O с вершиной в начале координат Рис Найдем точки пересечения этих линий: Возводя обе части уравнения в квадрат получим Отсюда Таким образом линии и пересекаются в точках О; и А; Проведя прямую параллельную O и пересекающую область видим что линия входа а линия выхода

5 Таким образом: поэтому f f г Построим треугольник рис Из чертежа ясно что внутри области Прямая параллельная O и пересекающая область входит в треугольник по стороне АС и выходит по стороне АВ Уравнение прямой проходящей через две точки M и M имеет вид Воспользовавшись этой формулой напишем уравнения сторон АВ и АС: АВ: откуда те; 6 АС: откуда те Таким образом: Поэтому f f д Построим область Для этого преобразуем уравнение границы: Выделим полный квадрат относительно переменной: Получившееся уравнение задает окружность радиусом с центром в точке; рис Рис Рис Чтобы расставить пределы интегрирования надо записать уравнения верхней и нижней половины окружности линии входа в область и выхода из области Разрешим исходное уравнение относительно: ±

6 Очевидно что верхней половине окружности соответствует уравнение нижней Таким образом: поэтому f f Пример Переменить порядок интегрирования: б 6 ; f f ; а в f f Решение: а Область интегрирования задается системой неравенств: Построим область рис6: верхняя половина параболы нижняя половина параболы При перемене порядка интегрирования интеграл примет вид c f Рис 6 Найдем координаты точек пересечения параболы и прямой: ± Таким образом А; В; Проведем прямую параллельно оси O пересекающую область Линия входа этой в область парабола линия выхода прямая Таким образом область можно задать и системой неравенств: Тогда f f 6

7 б В данном случае область интегрирования задается системой неравенств: 6 Построим эту область рис7: 6 гипербола прямая Найдем координаты точек А и В В точке А следовательно В точке В следовательно Таким образом А; В; При перемене порядка интегрирования интеграл примет вид f Рис 7 c Так как то c ; Проведем прямую параллельную оси O и пересекающую область Линия 6 входа гипербола откуда Линия выхода прямая откуда 6 Область задается неравенствами: 6 Окончательно получим 6 6 f f в Построим области: и: Граница области определяется уравнением ± Возводя обе части уравнения в квадрат получим уравнение параболы вершина кото- рой находится в точке; а осью симметрии является ось O Рис Граница области задается следующими уравнениями: прямая проходящая через начало координат и верхняя ветвь параболы Таким образом область интегрирования рис 7

8 Чтобы расставить пределы интегрирования найдем координаты точек пересечения линий границы Для этого решим систему уравнений; Отсюда Таким образом А; В; При перемене порядка интегрирования внешний интеграл будем брать по переменной внутренний по Поэтому проведем прямую пересекающую область и параллельную оси Ох Она входит в область по линии и выходит по линии Итак меняя порядок интегрирования получаем f f f Здесь перемена порядка интегрирования упрощает выкладки так как вместо вычисления двух интегралов понадобится вычислить всего один Пример Вычислить; ; где область ограничена линиями Решение Построим область рис 9: прямая параллельная оси O и прямые проходящие через начало координат Для вычисления интеграла перейдем от двойного интеграла к повторному Так как область можно задать системой неравенств: то Рис 9 Вычисляем сначала внутренний интеграл считая постоянной величиной так как интегрирование ведется по переменной: Теперь осталось вычислить получившийся внешний интеграл:

9 Таким образом Пример Вычислить Решение Построим область: ось O прямая параллельная оси O прямая проходящая через начало координат рис Прямые и пересекаются в точке A ; Переходя к двукратному интегралу и вычисляя его получим если ограничена линиями по формулам приведения Рис 9

10 Задачи для самостоятельного решения Расставить пределы интегрирования в повторных интегралах к которым сводится f если область ограничена линиями: а; б; в; г; д треугольник АВС где А; В; С; Переменить порядок интегрирования: а f ; б f ; в f ; г f Вычислить двойные интегралы считая что область ограничена указанными линиями: а; 7 ; б; ; в; ; г е; 6 Ответы а f ; б f ; в г f ; д а f ; б f f ; в f ; г f а; 7 б; в; f 6 г е е f ;

11 ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ Если на плоскости заданы и декартова и полярная системы координат причем полюс совпадает с началом координат а полярная ось совмещена с осью Ох то для перехода к полярным координатам используют формулы Рис При этом если область ограничена лучами α β и кривыми рис то f β α f Решение примеров Пример Вычислить > Решение Построим область рис: окружность радиуса прямые проходящие через начало координат Так как область представляет собой часть круга удобно перейди к полярным координатам При этом полюс совместим с точкой О; а полярную ось пустим по оси O Тогда где область ограничена линиями Рис Теперь надо описать область в полярной системе координат Угол внутри области меняется от до см рис Прямая k наклонена к оси O

12 под углом тангенс которого равен k Поэтому tg ; tg Отсюда; Итак внутри области Луч исходящий из полюса О и пересекающий выходит из области по окружности уравнение которой в полярных координатах имеет вид Таким образом область описывается системой неравенств: Теперь легко расставить пределы в повторном интеграле и вычислить его Пример Вычислить е где кольцо Решение Так как область ограничена окружностями 9 и 9 рис удобно перейти к полярным координатам: Тогда уравнения границ примут вид; 9 Рис Чтобы расставить пределы интегрирования в повторном интеграле заметим что внутри области угол принимает все значения от до Проведем из начала координат луч пересекающий область Он входит в область по линии и выходит по линии Таким образом: Тогда

13 9 9 9 е е е е е е е е е е е е Пример Вычислить если определяется неравенствами: Решение Построим область Для этого преобразуем уравнение границы: Итак граница это окружность радиуса с центром в точке; Так как то верхняя половина круга рис Перейдем к полярным координатам: Рис Уравнение границы в полярных координатах примет вид Полагая получим Область целиком расположена в первой четверти поэтому Таким образом в полярных координатах область задается неравенствами Теперь можно вычислить двойной интеграл

14 Задачи для самостоятельного решения Вычислить переходя к полярным координатам: где верхняя половина круга 6 где область удовлетворяет неравенствам где область ограничена линиями 9 6 где ограничена линиями 6 где область ограничена кривыми Ответы; ; ; ; ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ Двойной интеграл применяется при вычислении: а площади плоской фигуры ограниченной областью: S ; б объема цилиндрического тела ограниченного сверху непрерывной поверхностью f снизу плоскостью и сбоку прямой цилиндрической поверхностью вырезающей на плоскости O область:

15 f ; в площади поверхности заданной уравнением f проекцией которой на плоскость O является область: σ Кроме того двойные интегралы используются в механике для вычисления: а массы плоской пластинки занимающей область плоскости O и имеющей переменную поверхностную плотность γ γ: M γ ; б статистических моментов пластинки относительно осей O и O: ; M γ ; M γ в координат центра тяжести пластинки: γ M ц; M γ Решение примеров ц M M γ γ 6 Пример Найти площадь области ограниченной линиями Решение Построим область Уравнение задает параболу уравнение прямую проходящую через начало координат рис Чтобы найти точки пересечения этих линий решим систему уравнений: Отсюда Тогда Таким образом прямая пересекает параболу в точках; и А; По формуле S Рис Пример Найти площадь фигуры ограниченной линиями вне первой окружности;

16 Решение Уравнение задает окружность радиуса с центром в начале координат Уравнение задает окружность радиуса с центром в точке;: Требуется найти площадь фигуры AmBnА рис 6 Здесь удобно перейти к полярным координатам Тогда первое уравнение примет вид Второе уравнение: Рис 6 Чтобы определить координаты точек А и В решим совместно систему уравнений ± Итак; А; В Область AmBn можно задать неравенствами По формуле 6 S Пример Найти объем тела ограниченного координатными плоскостями и плоскостью Решение Построим тело рис 7 и его проекцию на плоскость O рис 6

17 По формуле Рис 7 Рис В примере область это треугольник ОАВ изображенный на рис а поверхность определяется уравнением плоскости откуда Таким образом Пример Найти объем тела ограниченного координатными плоскостями плоскостью и поверхностью Решение Тело изображено на рис 9 Плоскость проходит параллельно оси O; параболоид вершина которого находится в точке;; Проекцией тела на плоскость O является треугольник АВО рис АВ линия пересечения плоскости с плоскостью поэтому уравнение прямой AB: откуда 7

18 По формуле Рис 9 Рис цилиндром 6 Пример Найти объем тела ограниченного параболоидом и плоскостями и Решение Тело изображено на рис Для удобства расстановки пределов интегрирования построим проекцию тела на плоскость O рис По формуле Рис Рис

19 7 6 Пример 6 Найти объем тела ограниченного поверхностями 7 Решение Данное тело ограничено двумя параболоидами рис Линия пересечения параболоидов определяется системой уравнений Из первого уравнения Итак линией пересечения является окружность радиуса лежащая в плоскости: Проекция этой линии на плоскость O тоже окружность поэтому удобно перейти к полярным координатам Рис Объем тела можно подсчитать как разность объемов двух цилиндрических тел: Пример 7 Найти площадь поверхности сферы внутри цилиндра 9 Решение Цилиндр вырезает на поверхности сферы две части симметричные относительно плоскости O рис В силу симметрии достаточно вычислить площадь поверхности только верхней «шапочки» и результат удвоить 9

20 Для вычисления воспользуемся формулой Так как в нее входят частные производные вычислим и У нас поэтому из уравнения сферы Тогда Рис Таким образом по формуле σ Проекция поверхности на плоскость O круг удобно перейти к полярным координатам В полярной системе координат уравнение окружности вид Итак в полярных координатах σ 9 следовательно 9 примет Так как мы считали площадь только верхней «шапочки» то вся площадь поверхности равна σ σ n Пример Найти центр тяжести однородной пластинки ABC если A;- B; C; ;- Решение Для вычисления координат центра тяжести воспользуемся формулами 6 Так как пластинка однородна то поверхностная плотность γ постоянна поэтому формулы примут вид ц; ц

21 Из рисунка рис видно что пластинка имеет форму трапеции и симметрична относительно оси O поэтому Запишем уравнения прямых BC и A воспользовавшись формулой определяющей уравнение прямой проходящей через две заданные точки: ц BC: ; A: Рис Вычислим теперь отдельно числитель и знаменатель дроби определяющей координату: ц 9 В знаменателе стоит интеграл равный площади области те площади трапеции ABC Поэтому h ; можно вычислить этот AB C интеграл и непосредственно Таким образом ц; ц Пример 9 Найти массу верхней половины эллипса если плотность в каждой точке равна ординате точки b a Решение Плотность в каждой точке равна ординате те γ По формуле M γ Для верхней половины эллипса рис 6 b поэтому a Рис 6

22 M a a a a b a b a a a b a a a b a a a a b Задачи для самостоятельного решения a ab Найти площадь фигуры ограниченной линиями: а; б; в a ; г a a ; д Найти объем тела ограниченного поверхностями: а; б; в a ; г Найти площадь указанной поверхности: а части плоскости 6 заключенной в первом октанте; б части плоскости a вырезаемой цилиндром a ; в параболоида внутри цилиндра; г параболоида отсекаемого параболическим цилиндром и плоскостью Найти центр тяжести трапеции ABC где A; B; C; ; если плотность в каждой точке равна абсциссе этой точки Найти центр тяжести однородной фигуры ограниченной параболой и прямой 6 Найти массу круглой пластинки радиуса если поверхностная плотность в каждой точке пропорциональна расстоянию от центра круга Ответы а; б; в; г a a ; д 6 а 6; б; в a ; г a a

23 а; б a ; в; г ц ц ц ц 6 6 k ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ Для вычисления тройного интеграла его представляют в виде трехкратного интеграла: Решение примеров Пример Перейти от f b a f f к трехкратному и расставить пределы интегрирования если область ограничена: а плоскостью и координатными плоскостями; б конусом и плоскостью h; в шаром Решение а Построим область и проекцию этой области на плоскость O рис 7 Прямая АВ это линия пересечения плоскости с плоскостью поэтому ее уравнение Таким образом это ОАВ Рис 7 Рис Из рис легко увидеть что Проведя прямую параллельную оси O и пересекающую треугольник ОАВ рис замечаем что она входит в по линии а выходит по линии те

24 Чтобы выяснить пределы изменения проведем прямую параллельную оси O и пересекающую область рис 7 Она входит в область по поверхности и выходит по поверхности те Таким образом область можно описать системой неравенств 6 поэтому f f 6 б Для расстановки пределов в трехкратном интеграле построим область и ее проекцию на плоскость O область рис 9 Уравнение линии ограничивающей область получают решая систему уравнений h h Рис 9 То есть круг радиусом h с центром в начале координат Проводя прямые параллельные O и O пересекающие и получаем что описывается системой неравенств h h h h h Поэтому h h h h h f f

25 Можно выбрать в трехкратном интеграле другой порядок интегрирования тогда естественно изменятся и пределы интегрирования Например представим исходный интеграл в виде c f Чтобы расставить пределы интегрирования спроектируем на плоскость O и проведем прямые параллельные O и O и пересекающие соответственно и рис В этом случае задается неравенствами: h поэтому h f f Рис в Построим область и ее проекцию на плоскость O рис Рис Из чертежа видно что

26 f f f f Пример Вычислить если тело ограничено координатными плоскостями плоскостью и конусом Решение Построим тело и его проекцию на плоскость O рис Из чертежа видно что описывается неравенствами: Рис Таким образом 6 6

27 Задачи для самостоятельного решения Перейти от f к трехкратному интегралу и расставить пределы интегрирования если тело ограничено: а эллипсоидом; 9 б параболоидом и плоскостью; в координатными плоскостями и плоскостью 6 Вычислить если тело ограничено плоскостями и сферой Вычислить если тело ограничено плоскостями Вычислить и конусом Ответы 9 если тело ограничено плоскостями а f ; б f ; в f 6 ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ ЦИЛИНДРИЧЕСКИЕ И СФЕРИЧЕСКИЕ КООРДИНАТЫ Формулы перехода к цилиндрическим координатам рис: ; ; ; Формулы перехода к сферическим координатам θ r рис: r θ ; r θ ; r θ ; r θrθ Здесь; θ ; r 7

28 Решение примеров Пример Вычислить Рис Рис если ограничено конусом и плоскостью Решение Тело изображено на рис Линия пересечения конуса и плоскости имеет уравнение те Таким образом проекция тела на плоскость O круг рис6 Рис Рис 6 Перейдем к цилиндрическим координатам: ; ; ; В этих координатах уравнение окружности изображенной на рис 6 уравнение конуса а тело задается неравенствами; ; Итак

29 v Пример Вычислить если тело ограничено поверх- ностями Решение Построим область; плоскости Чтобы построить поверхность преобразуем уравнение: Это уравнение определяет круговой цилиндр в основании которого лежит круг радиуса с центром в точке;; Таким образом область интегрирования это цилиндр рис 7 Поэтому удобно воспользоваться цилиндрическими координатами В этих координатах уравнение цилиндрической поверхности ограничивающей область интегрирования примет вид То есть откуда Исходя из этого область можно описать системой неравенств; ; Рис 7 9

30 Итак Пример Вычислить где тело верхняя половина шара Решение Так как здесь область интегрирования является частью шара удобно перейти к сферическим координатам: r r r r r r r r r r r r r θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ Задачи для самостоятельного решения Вычислить если ограничено поверхностями Вычислить где ограничено поверхностями

31 Вычислить Вычислить если ограничено поверхностями если шар Ответы ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ Тройной интеграл применяется при вычислении: а объема тела Ω: ; 7 Ω б массы тела занимающего область Ω с переменной объемной плотностью γ: M γ ; Ω в координат центра тяжести тела Ω: ц γ M Ω ц γ 9 M Ω ц γ M Ω где М масса тела Если тело однородно то в формулах 9 можно положить γ ; M Решение примеров Пример Найти объем тела ограниченного цилиндром и плоскостями Решение Тело и его проекция на плоскость O изображены на рис Рис Чтобы найти координаты точек А и В решим систему уравнений:

32 ± A ; B; Таким образом область Ω описывается системой неравенств; ; По формуле 7 Ω Пример Найти массу тела ограниченного плоскостями если плотность в каждой точке γ Решение Построим тело Ω и его проекцию на плоскость O рис 9 Рис 9 Плоскость пересекается с плоскостью по прямой Решив систему получим координаты точки А; Таким образом тело Ω описывается системой неравенств; ; По формуле масса тела M Ω Пример Вычислить массу тела ограниченного плоскостями 9 и параболическим цилиндром если плотность в каждой точке пропорциональна абсциссе и на единице расстояния от плоскости O равна

33 Решение Плотность пропорциональна абсциссе; следовательно k γ На единице расстояния от плоскости O плотность равна; следовательно при γ Тогда k k Таким образом γ Построим тело Ω и его проекцию на плоскость O рис Рис Чтобы найти координаты точки А решим систему уравнений; 9 A Таким образом область можно задать системой неравенств Ω Ω 9: По формуле масса тела равна Ω M Пример Найти координаты центра тяжести тела ограниченного нижней половиной сферы и параболоидом если плотность в каждой точке пропорциональна квадрату расстояния от оси O

34 Решение Построим тело Вершина параболоида точке; ; Уравнение находится в можно преобразовать к виду те оно задает сферу радиуса с центром в точке; ; Итак тело имеет вид представленный на рис Проекцией этого тела на плоскость O является окружность Ее уравнение можно получить решив систему уравнений В плоскости уравнение линии пересечения имеет вид Уравнение проекции тела Ω на плоскость имеет тот же вид Ω Рис Поскольку окружность удобно при вычислении перейти к цилиндрическим координатам; ; В этих координатах уравнение границы Ω имеет вид; а угол удовлетворяет условию Уравнение параболоида в цилиндрических координатах откуда Уравнение сферы: ± Для нижней половины Переменная плотность по условию задачи пропорциональна квадрату расстояния от оси O те γ k В цилиндрических координатах γ k Так как тело симметрично относительно оси O то очевидно что центр тяжести лежит на этой оси те ц; ц Для вычисления ц воспользуемся формулой 9: ц γ M Ω Вычислим сначала массу тела M [формула ]:

35 6 k k k k k k k k M γ Ω Ω Ω Теперь вычислим Ω Ω Ω γ k k k k k k k k k k По формуле k k ц Итак центр тяжести рассматриваемого тела имеет координаты; ; 7

36 Задачи для самостоятельного решения 6 Найти объем тела ограниченного: а плоскостями; б параболоидом и плоскостью; в поверхностями и 6 Найти массу тела ограниченного: а сферами если плотность γ k ; б поверхностями если плотность γ k ; в конусом и плоскостью b если плотность пропорциональна ординате точки и на единице расстояния от плоскости O равна γ 6 Найти координаты центра тяжести однородного тела ограниченного плоскостями a Ответы 6 а; б; в 6 9 k γb 6 а k ; б; в 6 6 C ;; 6

37 Вариант ПРИЛОЖЕНИЕ ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности цилиндра заключенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного сферой и параболоидом если плотность в любой точке равна аппликате этой точки Вариант Найти центр тяжести плоской фигуры ограниченной линией и одной полуволной синусоиды Найти площадь поверхности конуса отсеченную плоскостями Найти объем тела ограниченного поверхностями Найти массу тела ограниченного частью шара радиуса находящейся в первом октанте если плотность в любой точке равна расстоянию от точки до плоскости O Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности конуса внутри цилиндра 9 Найти объем тела ограниченного поверхностями 9 9 Найти массу тела ограниченного сферическим слоем между поверхностями 9 и 6 если плотность в каждой точке обратно пропорциональна расстоянию от точки до начала координат Вариант Найти центр тяжести плоской фигуры ограниченной линиями 6 > Найти площадь поверхности расположенную внутри цилиндра 6 Найти объем тела ограниченного поверхностями 7

38 Найти массу тела ограниченного прямым круговым цилиндром радиуса высотой если плотность в каждой точке равна квадрату расстояния от точки до оси симметрии цилиндра Вариант Найти центр тяжести плоской фигуры ограниченной окружностью с центром в начале координат радиусом и двумя лучами расположенными симметрично относительно оси O и образующими между собой угол Найти площадь поверхности конуса расположенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного координатными плоскостями и плоскостью 6 если плотность в каждой точке равна абсциссе этой точки Вариант 6 Найти центр тяжести плоской фигуры ограниченной осью O и верхней частью эллипса b a Найти площадь поверхности цилиндра отсеченную плоскостями Найти объем тела ограниченного поверхностями 6 Найти массу тела ограниченного поверхностями 6 если плотность в каждой точке равна аппликате этой точки Вариант 7 Найти центр тяжести плоской фигуры ограниченной кардиоидой 7 Найти площадь поверхности конуса вырезанную цилиндром Указание Перейти к полярным координатам Найти объем тела ограниченного поверхностями Найти массу тела ограниченного поверхностями > если плотность равна ординате точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями p

39 Найти площадь поверхности параболоида внутри цилиндра Найти объем тела ограниченного поверхностями 6 Найти массу тела ограниченного поверхностями если плотность в каждой точке равна Вариант 9 Найти центр тяжести плоской фигуры ограниченной линиями 9 9 > Найти площадь поверхности тела ограниченного сферой и параболоидом Найти объем тела ограниченного поверхностями 6 9 вне цилиндра Найти массу тела ограниченного сферическим слоем между поверхностями 6 если плотность обратно пропорциональна расстоянию точки от начала координат Вариант Найти центр тяжести плоской фигуры ограниченной линией и прямой ОА проходящей через начало координат и точку A ; Найти площадь поверхности сферы вырезанную цилиндром Найти объем тела ограниченного поверхностями; внутри цилиндров Найти массу тела ограниченного шаром радиусом если плотность пропорциональна кубу расстояния от центра шара и на единице расстояния равна γ ; Вариант Найти центр тяжести плоской фигуры ограниченной линиями 6 Найти площадь поверхности цилиндра между плоскостями Найти объем тела ограниченного поверхностями Найти массу тела ограниченного цилиндрической поверхностью и плоскостями если плотность равна ординате точки 9

40 Вариант Найти центр тяжести плоской фигуры ограниченной кардиоидой Найти площадь поверхности шара заключенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного октантом шара координатными плоскостями и плоскостью если плотность в каждой точке равна аппликате этой точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности параболоида заключенную между цилиндром и плоскостью c a b Найти массу тела ограниченного параболоидом и плоскостью если плотность равна сумме квадратов координат точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности цилиндра заключенную между плоскостью O и поверхностью Найти объем тела ограниченного поверхностями Найти массу тела ограниченного цилиндром 6 если плотность пропорциональна квадрату расстояния от точки до оси цилиндра Вариант Найти центр тяжести плоской фигуры ограниченной линиями α α tg tg Найти площадь поверхности конуса расположенную внутри цилиндра Найти объем тела ограниченного поверхностями

41 Найти массу тела ограниченного поверхностями > если плотность равна ординате точки Вариант 6 Найти центр тяжести плоской фигуры ограниченной линиями 6 Найти площадь поверхности шара 6 внутри цилиндров Найти объем тела ограниченного поверхностями b a a b Найти массу тела ограниченного поверхностями если плотность равна аппликате точки Вариант 7 Найти центр тяжести равнобедренного прямоугольного треугольника с катетом если плотность в каждой точке пропорциональна квадрату расстояния от вершины прямого угла Найти площадь поверхности конуса вырезанную цилиндром Указание Перейти к полярным координатам Найти объем тела ограниченного поверхностями 9 Найти массу шара радиуса если плотность пропорциональна кубу расстояния от центра шара и на единице расстояния равна γ Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности параболоида заключенную в первом октанте Параболоид ограничен плоскостью 6 Найти объем тела ограниченного поверхностями 6 Найти массу части шара радиуса находящейся в первом октанте если плотность в каждой точке равна расстоянию от плоскости O Вариант 9 Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности тела ограниченного сферой и параболоидом

42 Найти объем тела ограниченного поверхностями Найти массу тела ограниченного прямым круговым цилиндром радиусом высотой если плотность равна квадрату расстояния точки от центра основания цилиндра Вариант Найти центр тяжести плоской фигуры ограниченной линиями > Найти площадь поверхности сферы 9 вырезанную цилиндром Найти объем тела ограниченного поверхностями Найти массу шара радиуса если плотность пропорциональна кубу расстояния от центра и на единице расстояния равна γ Вариант Найти центр тяжести плоской фигуры ограниченной линиями ± tg 6 Найти площадь поверхности цилиндра внутри цилиндра Найти объем тела ограниченного поверхностями внутри цилиндра Найти массу тела ограниченного общей частью двух шаров если плотность пропорциональна расстоянию от точки до плоскости O Вариант Найти центр тяжести плоской фигуры ограниченной кардиоидой Найти площадь поверхности конуса отсеченную плоскостями Найти объем тела ограниченного поверхностями вне цилиндра 6 Найти массу части шара радиуса находящейся в первом октанте если плотность в каждой точке равна расстоянию до плоскости O

43 Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности параболоида 6 заключенную между цилиндром и плоскостью Найти объем тела ограниченного поверхностями Найти массу тела ограниченного сферическим слоем между поверхностями 6 если плотность обратно пропорциональна расстоянию от начала координат Вариант Найти центр тяжести плоской фигуры ограниченной линиями 9 Найти площадь поверхности расположенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного параболоидом и плоскостью если плотность равна сумме квадратов координат точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности конуса внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного общей частью двух шаров если плотность пропорциональна расстоянию от точки до плоскости O

44 СОДЕРЖАНИЕ ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ ЦИЛИНДРИЧЕСКИЕ И СФЕРИЧЕСКИЕ КООРДИНАТЫ 7 6 ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ ПРИЛОЖЕНИЕ ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ 7 Учебное издание КРАТНЫЕ ИНТЕГРАЛЫ задачи и упражнения Методические указания Составитель Карпилова Ольга Михайловна Редактор Ю Н Л и т в и н о в а Доверстка Ю Н Л и т в и н о в а Подписано в печать Формат 6х /6 Бумага офсетная Печать офсетная Усл печ л 7 Тираж экз Заказ Арт С-9/ Самарский государственный аэрокосмический университет 6 Самара Московское шоссе Изд-во Самарского государственного аэрокосмического университета 6 Самара Московское шоссе

Cos, sin, J dd dd d d 5 Вычислить zdd zddz ddz, где внешняя сторона поверхности z, отсекаемая плоскостью z Р е ш е н и е Поверхность представляет собой параболоид, заданный явно уравнением z Поэтому

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ» Кафедра «Высшая математика» ВЫСШАЯ МАТЕМАТИКА. МАТЕМАТИКА. МАТЕМАТИКА (СПЕЦГЛАВЫ). МАТЕМАТИЧЕСКИЙ АНАЛИЗ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАСЧЕТНЫМ ЗАДАНИЯМ ПО КУРСУ ВЫСШЕЙ МАТЕМАТИКИ «ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РЯДЫ КРАТНЫЕ ИНТЕГРАЛЫ» ЧАСТЬ III ТЕМА КРАТНЫЕ ИНТЕГРАЛЫ ОГЛАВЛЕНИЕ Вычисление двойных и тройных

Министерство транспорта Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Российский университет транспорта (МИИТ)» ИТТСУ Кафедра «Высшая и вычислительная

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 9 Вычисление двойного интеграла в полярных координатах Приложения двойных интегралов Рассмотрим частный случай замены переменных часто используемый при вычислении двойного интеграла

Двойные интегралы Примеры решения задач 1. Свести двойной интеграл f(x, y) dx dy к повторному двумя способами (по формуле (1) и по формуле (2)), если G область, ограниченная кривыми x = 1, y = x 2, y =

Выражение массы тела через тройной интеграл в цилиндрических координатах Определения и формулы для решения задач Определение Цилиндрическим брусом ориентированным по оси O рис Называется тело G ограниченное

Министерство образования Республики Беларусь БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра инженерной математики Н.А. Кондратьева О.Г. Вишневская Н.К. Прихач МАТЕМАТИКА Методическое пособие

Пособие предназначено для студентов заочников КГТУ второго года обучения. В пособии в краткой и доступной форме рассмотрены темы: Кратные интегралы, Криволинейные интегралы, Ряды, Теория вероятностей.

Министерство науки и образования Российской Федерации Московский Государственный Университет Геодезии и Картографии АВ Аристархова, НГ Бабаева Индивидуальные задания по высшей математике КРАТНЫЕ ИНТЕГРАЛЫ

БАНК ЗАДАЧ ПО ТЕМЕ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ» * Изменить порядок интегрирования + d d * Найти площадь плоской области, ограниченной линиями =, =, = * Вычислить (D) + acctg d, где) +, + 9, = (D область,

МИНИСТЕРСТВО КУЛЬТУРЫ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КИНО И

Часть. Примерные экзаменационные задачи по математике А. Простейшие задания на три балла.. Вычислить интегралы arcsin д) II семестр ИСиА, и 9 гр. и) 6 n к) 5 6 5 ж) 6 г) cos з) z arcsin z. Вычислить производную

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)» Институт транспортной техники

3 область (D) В нашем случае n - вектор нормали к плоскости XOY те n k { } = ϕ, ϕ, Тогда = =, а n { } cos γ =, + + (ϕ) (ϕ) (ϕ) (ϕ) dq = + + dd Замечание Если поверхность (Q) правильная в направлении

ЗАДАЧНИК ПО МАТЕМАТИКЕ (тенические факультеты, семестр) 7 Интегралы Найдите интегралы d d sin + d + + d + d + d 7 (+) d + + 8 d 9 cos d cos + d cos d + 8 d 9 d d + d 9 + d + 7 tg d 8 cosd cos sin 9 d

ЛЕКЦИЯ N 45 Кратные интегралы в полярных, цилиндрических и сферических координатах Приложения кратных интегралов Двойной интеграл в полярных координатах Тройной интеграл в цилиндрических и сферических

Глава. Кратные интегралы.. Занятие... Сведение двойного интеграла к повторному При вычислении двойных интегралов следует различать два случая. () Первый случай. Область интегрирования ограничена слева

ВЫСШИЙ КОЛЛЕДЖ СВЯЗИ СБОРНИК ТИПОВЫХ РАСЧЕТОВ по дисциплине «ВЫСШАЯ МАТЕМАТИКА» часть II для студентов специальности Т 000 Почтовая связь Минск 00 Составитель Рябенкова ЛА Издание утверждено на заседании

ЛЕКЦИЯ Линии второго порядка гиперболу В качестве примера найдем уравнения задающие окружность, параболу, эллипс и Окружность Окружностью называется множество точек плоскости, равноудалённых от заданной

Тройной интеграл Волченко Ю.М. Содержание лекции Понятие тройного интеграла. Условия его существования. Теорема о среднем. Вычисление тройного интеграла в декартовых и криволинейных координатах. Тройной

ЛЕКЦИЯ N. Вычисление кратных интегралов..вычисление двойного интеграла в прямоугольных декартовых координатах.....вычисление двойного интеграла (произвольная область).....тройной интеграл.....вычисление

Введение Методические указания содержат 26 вариантов индивидуальных домашних заданий по темам «Прямая на плоскости и в пространстве», «Плоскость», «Кривые и поверхности второго порядка». Под индивидуальными

Содержание Введение Кратные, криволинейные и поверхностные интегралы Элементы теории поля Задачи для аудиторных занятий Краткие сведения из теории Образцы решения задач Задачи для самоподготовки Тестовая

Практическое занятие 6 Поверхностные интегралы 6 Определение свойства вычисление и приложения поверхностного интеграла -го рода 6 Определение свойства и вычисление поверхностного интеграла -го рода 6 Определение

Б. М. Маврин, Е. И. Балаев ИЗОБРАЖЕНИЕ ТЕЛ ВРАЩЕНИЯ Практикум Самара 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ

Двойные интегралы Задачи и упражнения для самостоятельной работы 1. Сведите двойной интеграл f(x, y) dx dy к повторному двумя способами, если: G а) G треугольник с вершинами (1, 1), (4, 1), (4, 4); б)

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика» И Н Пирогова Аналитическая геометрия в примерах и задачах Екатеринбург

Занятия 1-2. Определенный интеграл и его приложения I. Используя формулу Ньютона-Лейбница, вычислить определенный интеграл: 1. (2 + 2) 2. / 3. (4.) 5. 6. 7. 8. Ефимов-Поспелов 7.324-7.352, 7.380-7.385,

Лекция 7 Несобственные интегралы Несобственными интегралами называются определенные интегралы, для которых не выполнено хотя бы одно из условий существования определенного (собственного) интеграла:)либо

14-е занятие. Тройные интегралы Матем. анализ, прикл. матем., 3-й семестр Повторение A1 В следующем интеграле перейти к полярным координатам и расставить пределы интегрирования в том и другом порядке:

Министерство образования Российской Федерации Ярославский государственный университет им. П.Г. Демидова Кафедра дискретного анализа ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ Задачи Ярославль Составитель канд.

МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ) ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Варианты контрольных заданий Задачник МОСКОВСКИЙ АВТОМОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая и прикладная математика» П И Гниломедов ПРИЛОЖЕНИЯ КРАТНЫХ И КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени

Приложение 5 Министерство сельского хозяйства Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Саратовский государственный аграрный университет

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ. Прямая линия 1. Вычислите периметр треугольника, вершинами которого служат точки A(6; 7), B(3; 3), C(1; 5). 2. Найдите точку, равноудаленную от точек A(7;

Министерство образования и науки Российской Федерации Ярославский государственный университет им. П. Г. Демидова Кафедра алгебры и математической логики Кривые второго порядка Часть I Методические указания

Содержание Кратные интегралы Понятие кратного интеграла Двойные интегралы. Области на плоскости................. Повторный интеграл................ 3.3 Вычисление двойного интеграла в декартовых координатах.......................

Практическое занятие 14 Тема: Парабола План 1. Определение и каноническое уравнение параболы.. Геометрические свойства параболы. Взаимное расположение параболы и прямой, проходящей через ее центр. Основные

1 Простейшие задачи аналитической геометрии на плоскости 11 Расстояние между двумя точками Рассмотрим прямоугольную систему координат (декартовую, рис Рис 1 Любой точки M соответствуют координаты OA x

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКОЕ ВЫСШЕЕ АВИАЦИОННОЕ УЧИЛИЩЕ ГРАЖДАНСКОЙ АВИАЦИИ (ИНСТИТУТ)

Глава 5. Тройной интеграл. 5.1. Определение тройного интеграла. После введения в предыдущей главе понятия двойного интеграла естественно было бы провести его дальнейшее обобщение на трехмерное пространство

АЛГЕБРАИЧЕСКИЕ ЛИНИИ НА ПЛОСКОСТИ.. ЛИНИИ ПЕРВОГО ПОРЯДКА (ПРЯМЫЕ НА ПЛОСКОСТИ... ОСНОВНЫЕ ТИПЫ УРАВНЕНИЙ ПРЯМЫХ НА ПЛОСКОСТИ Ненулевой вектор n перпендикулярный заданной прямой называется нормальным

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ ИМГУБКИНА ТС Филиппова АНФилиппов МЕТОДИЧЕСКИЕ УКАЗАНИЯ к изучению темы «Кратные и криволинейные

Пензенский государственный педагогический университет имени ВГБелинского ОГНикитина ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Учебное пособие Пенза Печатается по решению редакционно-издательского

Тема ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ Лекция.. Прямые на плоскости П л а н. Метод координат на плоскости.. Прямая в декартовых координатах.. Условие параллельности и перпендикулярности

ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Московский государственный технический университет имени Н.Э. Баумана Факультет «Фундаментальные науки» Кафедра «Математическое моделирование» À.Í. Êàíàòíèêîâ, À.Ï. Êðèùåíêî

Глава 5 Поверхностные интегралы -го типа (продолжение) 5 Задачи в классе Задача 5 (4349) Вычислить интеграл где часть поверхности конуса z d, x = ρ cos ϕ sin α, y = ρ sin ϕ sin α, z = ρ cos α ((ρ h,

Федеральное агентство по образованию Уральский государственный лесотехнический университет Кафедра Сопротивления материалов и теоретической механики В. А. Калентьев В. М. Калинин Л. Т. Раевская Н. И. Чащин

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ЗАНЯТИЕ ПЛОСКОСТЬ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ Написать векторное уравнение плоскости и объяснить смысл величин, входящих в это уравнение Написать общее уравнение плоскости

3 Пример Записать выражения для статических моментов плоской материальной области (D) На основании формул (3) с учетом фигуры (Φ) имеем: ρ, dd, ρ, dd Исходя из механического смысла статического момента,

Задача 1 Найти координаты центра тяжести полуокружности y = r 2 x 2. Задача 5 площадь части поверхности z = 1 4 xy, расположенной внутри поверхности x 2 + y 2 = 16. Задача 2 Изменить порядок интегрирования

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ НАЦИОНАЛЬНАЯ МЕТАЛЛУРГИЧЕСКАЯ АКАДЕМИЯ УКРАИНЫ МЕТОДИЧЕСКИЕ УКАЗАНИЯ к решению задач по дисциплине Высшая математика и варианты контрольных заданий практические

Практические занятия по курсу высшей математики (III семестр) на основе учебного пособия «Сборник индивидуальных заданий по высшей математике», том 3, под ред. Рябушко А.П. для студентов дневной формы

Московский государственный технический университет имени Н.Э. Баумана Факультет «Фундаментальные науки» Кафедра «Вычислительная математика и математическая физика» А.И. Левина КРАТНЫЕ ИНТЕГРАЛЫ Электронное

Интегральное исчисление функции нескольких переменных интегралов двойного тройного криволинейного по длине дуги (первого рода) поверхностного по площади поверхности (первого рода) Пусть функция f() определена

1.3. Занятие 3 1.3.1. Вычисление тройных интегралов в декартовых координатах Пусть пространственная область, D ее проекция на плоскость Oxy. Область называется -правильной, если любая вертикальная прямая

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Белорусский национальный технический университет Кафедра инженерной математики ВЫСШАЯ МАТЕМАТИКА Руководство к решению задач для студентов механико-технологического

Практическое занятие 1 Тема: Гипербола План 1 Определение и каноническое уравнение гиперболы Геометрические свойства гиперболы Взаимное расположение гиперболы и прямой, проходящей через ее центр Асимптоты

Раньше мы доказывали свойства определенного интеграла, пользуясь его определением, как предела сумм . Совершенно так же можно доказать и основные свойства кратных интегралов. Для простоты мы все функции будем считать непрерывными, так что интегралы от них безусловно имеют смысл.

I. Постоянный множитель можно выносить за знак интеграла, и интеграл от конечной суммы функций равен сумме интегралов от слагаемых:

II. Если область разложена на конечное число частей [например на две части , то интеграл по всей области равен сумме интегралов по всем частям:

III. Если в области , то

В частности :

IV. Если сохраняет знак в области (а), то имеет место теорема о среднем, выражающаяся формулой

где - некоторая точка, лежащая внутри области (а).

В частности, при получаем

где - площадь области .

Аналогичные свойства имеют место и для трехкратного интеграла. Заметим, что при определении двукратного и трехкратного интеграла как предела суммы считается всегда, что область интегрирования конечна и подынтегральная функция во всяком случае ограничена, т. е. существует такое положительное число А, что во всех точках N области интегрирования. Если эти условия не выполнены, то интеграл может существовать как несобственный интеграл аналогично тому, как это имело место для простого определенного интеграла . Мы займемся несобственными кратными интегралами в § 8.

Предостережение.При вычислении несобственных интегралов с особыми точками внутрипромежутка интегрирования нельзямеханически применять формулу Ньютона – Лейбница, поскольку это может привести к ошибкам.

Общее правило: формула Ньютона – Лейбница верна, если первообразная от f(x) в особой точке последней непрерывна.

Пример 2.11.

Рассмотрим несобственный интеграл с особой точкой х = 0. Формула Ньютона–Лейбница, применяемая формально, дает

Однако общее правило здесь не выполняется; для f(x) = 1/x первообразная ln |x| не определена в х = 0 и является бесконечно большой в этой точке, т.е. не является непрерывной в этой точке. Непосредственной проверкой легко убедиться, что интеграл расходится. Действительно,

Полученная неопределенность может быть раскрыта по-разному, поскольку e и d стремятся к нулю независимым образом. В частности, полагая e = d, получаем главное значение несобственного интеграла, равное 0. Если e = 1/n, а d =1/n 2 , т.е. d стремится к 0 быстрее, чем e, то получаем

при и , наоборот,

т.е. интеграл расходится.n

Пример 2.12.

Рассмотрим несобственный интеграл с особой точкой х = 0. Первообразная от функции имеет вид и непрерывна в точке х = 0. Поэтому можно применить формулу Ньютона – Лейбница:

Естественным обобщением понятия определенного интеграла Римана на случай функции нескольких переменных является понятие кратного интеграла. Для случая двух переменных такие интегралы называют двойными.

Рассмотрим в двумерном евклидовом пространстве R ´ R , т.е. на плоскости с декартовой системой координат, множество Е конечной площади S .

Обозначим через (i = 1, …, k ) разбиение множества Е , т.е. такую систему его подмножеств E i , i = 1,. . ., k , что Ø при i ¹ j и (рис. 2.5). Здесь через обозначено подмножество E i без его границы, т.е. внутренние точки подмножества E i , которые вместе с его границей Гр E i образуют замкнутое подмножество E i, . Ясно, что площадь S (E i) подмножества E i совпадает с площадью его внутренней части , поскольку площадь границы ГрE i равна нулю.

Через d(E i) обозначим диаметр множества E i , т.е. максимальное расстояние между двумя его точками. Величину l(t) = d(E i) назовем мелкостью разбиения t. Если функция f(x),x = (x, y), определена на E как функция двух аргументов, то всякую сумму вида

X i Î E i , i = 1, . . . , k, x i = (x i , y i),

зависящую как от функции f и разбиения t , так и от выбора точек x i Î E i Ì t, называют интегральной суммой функции f .

Если для функции f существует ,не зависящий ни от разбиений t , ни от выбора точек (i = 1, …, k), то этот предел называется двойным интегралом Римана от f(x,y) и обозначается

Саму функцию f называют в этом случае интегрируемой по Риману .

Напомним, что в случае функции одного аргумента в качестве множества Е , по которому производится интегрирование, обычно берется отрезок , а в качестве его разбиения t рассматривается разбиение, состоящее из отрезков. В остальном, как нетрудно убедиться, определение двойного интеграла Римана повторяет определение определенного интеграла Римана для функции одного аргумента.

Двойной интеграл Римана от ограниченных функций двух переменных обладает обычными свойствами определенного интеграла для функций одного аргумента – линейностью, аддитивностью относительно множеств, по которым производится интегрирование, сохранение при интегрировании нестрогих неравенств , интегрируемость произведения интегрируемых функций и т.п.

Вычисление кратных интегралов Римана сводится к вычислению повторных интегралов . Рассмотрим случай двойного интеграла Римана. Пусть функция f(x,y) определена на множестве Е, лежащем в декартовом произведении множеств X ´ Y, E Ì X ´ Y.

Повторным интегралом от функции f(x, y) называется интеграл, в котором последовательно выполняется интегрирование по разным переменным, т.е. интеграл вида

Множество E(y) = {x: Î E} Ì X называется сечением множества E, соответствующим заданному y, y Î E y ; множество E y называется – проекцией множества E на ось Y.

Для повторного интеграла используют также такое обозначение:

которое, как и прежнее, означает, что сначала при фиксированном y, y Î E y , проводится интегрирование функции f(x, y) по x по отрезку E (y ), являющемуся сечением множества Е , соответствующим этому y. В результате внутренний интеграл определяет некоторую функцию одной переменной – y. Эта функция интегрируется затем как функция одной переменной, на что указывает символ внешнего интеграла.

При изменении порядка интегрирования получается повторный интеграл вида

где внутреннее интегрирование проводится по y, а внешнее – по x. Как соотносится этот повторный интеграл с повторным интегралом, определенным выше?

Если существует двойной интеграл от функции f , т.е.

то существуют и оба повторных интеграла, причем они одинаковы по величине и равны двойному, т.е.

Подчеркнем, что сформулированное в этом утверждении условие возможности перемены порядка интегрирования в повторных интегралах является лишь достаточным , но не необходимым.

Другие достаточные условия возможности перемены порядка интегрирования в повторных интегралах формулируются следующим образом:

если существует хотя бы один из интегралов

то функция f(x, y) интегрируема по Риману на множестве Е , оба повторных интеграла от нее существуют и равны двойному интегралу. n

Конкретизируем записи проекций и сечений в обозначениях повторных интегралов.

Если множество Е является прямоугольником

то E x = {x: a £ x £ b}, E y = {y: c £ y £ d}; при этом E(y) = E x для любого y, y Î E y . , а E(x) = E y для любого x, x Î E x ..

Формальная запись: "y y Î E y Þ E(y) = E x Ù"x x Î E x Þ E(x) = E y

Если множество Е имеет криволинейную границу и допускает представления

В этом случае повторные интегралы записываются так:

Пример 2.13.

Вычислить двойной интеграл по прямоугольной области, сведя его к повторному .

Поскольку выполняется условие sin 2 (x+ y) =| sin 2 (x + y)|, то проверку выполнимости достаточных условий существования двойного интеграла I в форме существования любого из повторных интегралов

здесь проводить специально не следует и можно сразу переходить к вычислению повторного интеграла

Если он существует, то существует и двойной интеграл, причем I = I 1 . Поскольку

Итак, I = .n

Пример 2.14.

Вычислить двойной интеграл по треугольной области (см. рис. 2.6), сведя его к повторному

Гр(E) = {: x = 0, y = 0, x + y = 2}.

Сначала убедимся в существовании двойного интеграла I. Для этого достаточно убедиться в существовании повторного интеграла

т.е. подынтегральные функции непрерывны на отрезках интегрирования, поскольку все они степенные. Следовательно, интеграл I 1 существует. В этом случае двойной интеграл тоже существует и равен любому повторному, т.е.

Пример 2.15.

Для лучшего понимания связи между понятиями двойного и повторных интегралов рассмотрим следующий пример, который при первом чтении может быть опущен. Задана функция двух переменных f(x, y)

Отметим, что эта функция при фиксированном х нечетна по y , а при фиксированном y – нечетна по x. В качестве множества Е, по которому интегрируется эта функция, возьмем квадрат E = {: -1 £ x £ 1, -1 £ y £ 1 }.

Вначале рассмотрим повторный интеграл

Внутренний интеграл

берется при фиксированном y, -1 £ y £ 1. Поскольку подынтегральная функция при фиксированном y нечетная по x, а интегрирование по этой переменной осуществляется по отрезку [-1, 1], симметричному относительно точки 0, то внутренний интеграл равен 0. Очевидно, что внешний интеграл по переменной y от нулевой функции также равен 0, т.е.

Аналогичные рассуждения для второго повторного интеграла приводят к тому же результату:

Итак, для рассматриваемой функции f(x, y) повторные интегралы существуют и равны друг другу. Однако двойной интеграл от функции f(x, y) не существует. Чтобы убедиться в этом, обратимся к геометрическому смыслу вычисления повторных интегралов.

Для вычисления повторного интеграла

используется разбиение квадрата Е специального вида, равно как и специальным образом проводимый подсчет интегральных сумм. Именно, квадрат Е разбивается на горизонтальные полосы, (см. рис.2.7), а каждая полоса – на маленькие прямоугольники. Каждая полоска соответствует некоторому значению переменной y; например, это может быть ордината горизонтальной оси полосы.

Подсчет интегральных сумм производится так: сначала подсчитывается суммы для каждой полосы в отдельности, т.е. при фиксированном y для разных x, а затем эти промежуточные суммы суммируются для разных полос, т.е. для разных y. Если мелкость разбиения устремить к нулю, то в пределе мы получим указанный выше повторный интеграл.

Ясно, что для второго повторного интеграла

множество Е разбивается вертикальными полосами, соответствующими разным x. Промежуточные суммы подсчитываются внутри каждой полосы по маленьким прямоугольникам, т.е. по y, а затем они суммируются для разных полос, т.е. по х. В пределе, при мелкости разбиения, стремящейся к нулю, получаем соответствующий повторный интеграл.

Чтобы доказать, что двойной интеграл не существует, достаточно привести один пример разбиения, расчет интегральных сумм по которому в пределе при мелкости разбиения, стремящейся к нулю, дает результат, отличный от значения повторных интегралов. Приведем пример такого разбиения, соответствующего полярной системе координат (r, j) (см. рис. 2.8).

В полярной системе координат положение любой точки на плоскости М 0 (x 0 , y 0), где x 0 ,y 0 – декартовы координаты точки М 0 – определяется длиной r 0 радиуса, соединяющего ее с началом координат и углом j 0 , образуемым этим радиусом с положительным направлением оси x (угол отсчитывается против часовой стрелки). Связь между декартовыми и полярными координатами очевидна:

y 0 = r 0 × sinj 0 .

Разбиение строится следующим образом. Сначала квадрат Е разбивается на сектора радиусами, исходящими из центра координат, а затем каждый сектор – на маленькие трапеции линиями, перпендикулярными оси сектора. Подсчет интегральных сумм проводится так: сначала по маленьким трапециям внутри каждого сектора вдоль его оси (по r), а затем – по всем секторам (по j) . Положение каждого сектора характеризуется углом его оси j, а длина его оси r(j) зависит от этого угла:

если или , то ;

если , то ;

если , то

если , то .

Переходя к пределу интегральных сумм полярного разбиения при мелкости разбиения, стремящейся к нулю, получим запись двойного интеграла в полярных координатах. Такую запись можно получить и чисто формальным образом, заменяя декартовы координаты (x, y) на полярные (r, j).

По правилам перехода в интегралах от декартовых координат к полярным следует писать, по определению:

В полярных координатах функция f(x, y) запишется так:

Окончательно имеем

Внутренний интеграл (несобственный) в последней формуле

где функция r(j) указана выше, 0 £ j £ 2p , равен +¥ для любого j, ибо

Следовательно, подынтегральная функция во внешнем интеграле, вычисляемом по j, не определена ни для какого j . Но тогда не определен и сам внешний интеграл, т.е. не определен исходный двойной интеграл.

Отметим, что для функции f(x, y) не выполнено достаточное условие существования двойного интеграла по множеству Е. Покажем, что интеграл

не существует. Действительно,

Аналогично устанавливается такой же результат для интеграла

Остановимся несколько подробнее на работах Остроградского по кратным интегралам.

Формула Остроградского для преобразования тройного интеграла в двойной, которую мы пишем обычно в виде

где div A - дивергенция поля вектора А,

Аn - скалярное произведение вектора А на единичный вектор внешней нормали n граничной поверхности, в математической литературе нередко связывалась ранее с именами Гаусса и Грина.

На самом деле в работе Гаусса о притяжении сфероидов можно усмотреть только весьма частные случаи формулы (1), например при P=x, Q=R=0 и т. п. Что касается Дж. Грина, то в его труде по теории электричества и магнетизма формулы (1) вовсе нет; в нем выведено другое соотношение между тройным и двойным интегралами, именно, формула Грина для оператора Лапласа, которую можно записать в виде

Конечно, можно вывести формулу (1) и из (2), полагая

и точно так же можно получить формулу (2) из формулы (1), но Грин этого и не думал делать.

где слева стоит интеграл по объему, а справа интеграл по граничной поверхности, причем суть направляющие косинусы внешней нормали.

Парижские рукописи Остроградского свидетельствуют, с полной несомненностью, что ему принадлежит и открытие, и первое сообщение интегральной теоремы (1). Впервые она была высказана и доказана, точно так, как это делают теперь в “Доказательстве одной теоремы интегрального исчисления”, представленном Парижской Академии наук 13 февраля 1826 г., после чего еще раз была сформулирована в той части “Мемуара о распространении тепла внутри твердых тел ”, которую Остроградский представил 6 августа 1827 г. “Мемуар” был дан на отзыв Фурье и Пуассону, причем последний его, безусловно читал, как свидетельствует запись на первых страницах обеих частей рукописи. Разумеется, Пуассону и не приходила мысль приписывать себе теорему, с которой он познакомился в сочинении Остроградского за два года до представления своей работы на теории упругости.

Что касается взаимоотношения работ по кратным интегралам Остроградского и Грина, напомним, что в “Заметке по теории теплоты” выведена формула, обнимающая собственную формулу Грина, как весьма частный случай. Непривычная теперь символика Коши, употребленная Остроградским в “Заметке”, до недавнего времени скрывала от исследователей это важное открытие. Разумеется, за Грином остается честь открытия и первой публикации в 1828 г. носящей его имя формулы для операторов Лапласа.

Открытие формулы преобразования тройного интеграла в двойной помогло Остроградскому решить проблему варьирования п-кратного интеграла, именно, вывести понадобившуюся там общую формулу преобразования интеграла от выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид

Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала.

В “Мемуаре об исчислении вариаций кратных интегралов” рассмотрены еще два важных вопроса теории таких интегралов. Во-первых, Остроградский выводит формулу замены переменных в многомерном интеграле; во-вторых, впервые дает полное и точное описание приема вычисления п- кратного интеграла с помощью п последовательных интеграций по каждой из переменных в соответствующих пределах. Наконец, из формул, содержащихся в этом мемуаре, легко выводится общее правило дифференцирования по параметру многомерного интеграла, когда от этого параметра зависит не только подынтегральная функция, но и граница области интегрирования. Названное правило вытекает из наличных в мемуаре формул настолько естественным образом, что позднейшие математики даже отождествляли его с одною из формул этого мемуара.

Замене переменных в кратных интегралах Остроградский посвятил специальную работу. Для двойного интеграла соответствующее правило вывел с помощью формальных преобразований Эйлер, для тройного - Лагранж. Однако, хотя результат Лагранжа верен, рассуждения его были не точными: он как бы исходил из того, что элементы объемов в старых и новых переменных - координатах - между собою равны. Аналогичную ошибку допустил вначале в только что упомянутом выводе правила замены переменных Остроградский. В статье “О преобразовании переменных в кратных интегралах” Остроградский раскрыл ошибку Лагранжа, а также впервые изложил тот наглядный геометрический метод преобразования переменных в двойном интеграле, который, в несколько более строгом оформлении, излагается и в наших руководствах. Именно, при замене переменных в интеграле по формулам, область интегрирования разбивается координатными линиями двух систем u=const, v=const на бесконечно малые криволинейные четырехугольники. Тогда интеграл можно получить, складывая сначала те его элементы, которые отвечают бесконечно узкой криволинейной полосе, а затем, продолжая суммировать элементы полосами, пока они все не будут исчерпаны. Несложный подсчет дает для площади, которая с точностью до малых высшего порядка может рассматриваться как параллелограмм, выражение, где, выбирается так, чтобы площадь была положительной. В итоге получается известная формула

Для функции двух переменных, заданной как z = f (x , y ) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла , а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов , в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл , нужно свести его к повторному интегралу, который имеет вид

.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y

.

Пример 1. Вычислить двойной интеграл

Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

.

Пример 2. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

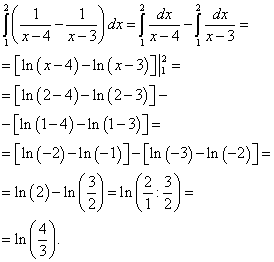
Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f (x , y ) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b , но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функций или - это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y . Тогда повторный интеграл будет иметь вид

.

Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

Пример 5. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

.

Вычисляем первое слагаемое:

Вычисляем второе слагаемое:

Вычисляем третье слагаемое:

Получаем сумму, которая и будет решением данного двойного интеграла:

.

Пример 6. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

x -правильная и неправильная, y -правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x , то область интегрирования называется x -неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x -правильной

Аналогично, если границу, заданную линиями, выраженными через y , прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y -неправильной. Вывести теперь признаки y -правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x -неправильными и y -правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y -неправильной, так как её нижнюю границу нельзя задать одной линией y = y (x ) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части - и .

Вычисляется этот двойной интеграл так:

Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О"Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О"Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О"Генри . Шехерезада с Мэдисон-сквера .)

Тогда, если левый интеграл у нас по переменной x , а правый - по y , то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции , разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8.

.

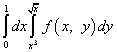Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

.

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x /2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

y ≤ 2x ;
y ≥ x /2;
y ≤ 2/x .

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x ) .